Einsums User Guide#

This guide is an overview and explains the important features; details are found in the reference. Follow the links below to find more information on the specific parts of Einsums.

Getting started

User's Reference

Extras

Einsums License

Design Goals#

The overall goal of Einsums is to allow scientists and mathematicians to write highly parallelized code without needing to become a wizard in high-performance computing. Another goal is to have an interface that mimics mathematical notation as closely as possible, so users don’t necessarily need to think about how to transform their equations into code. As an example, one might construct the Einstein tensor using the following equation.

\[G_{\mu\nu} = R_{\mu\nu} - \frac{1}{2} R g_{\mu\nu}\]

This would become the following code using Einsums.

Tensor ricci_tensor{"R", 4, 4}, metric_tensor{"g", 4, 4};
double ricci_curvature;
// Initializations of all of these.

Tensor einstein_tensor{"G", 4, 4};
einstein_tensor = ricci_tensor - 0.5 * ricci_curvature * metric_tensor;

Another example for a more general contraction is the coupled-cluster singles and doubles energy expression. The governing equation is this.

\[ \begin{align}\begin{aligned}E_{CCSD} = E_{HF} + \sum_{i}^{occ}\sum_{a}^{virt} F_{ia} t_{i}^{a} + \frac{1}{4}\sum_{ij}^{occ} \sum_{ab}^{virt} \left<ij\middle|\middle| ab\right> \tau_{ij}^{ab}\\\tau_{ij}^{ab} = t_{ij}^{ab} + 2t_{i}^{a}t_{j}^{b}\\\left<pq \middle|\middle| rs \right> = \left<pq\middle|\middle|rs\right> - \left<pq\middle|\middle|sr\right>\end{aligned}\end{align} \]

This becomes the following code.

double E_hf;
int n_occ; // The number of occupied orbitals.
int n_orbs; // The number of orbitals.
int n_virt = n_orbs - n_occ; // The number of virtual orbitals.
Tensor F{"F", n_orbs, n_orbs}; // The Fock matrix.
Tensor TEI{"G", n_orbs, n_orbs, n_orbs, n_orbs}; // The electron repulsion integrals.
Tensor t1_amps{"T1", n_occ, n_virt};
Tensor t2_amps{"T2", n_occ, n_occ, n_virt, n_virt};
// Populate these values.

double E_ccsd = E_hf;

// Defining an intermediate.
Tensor tau2{"tau2", n_occ, n_occ, n_virt, n_virt};
tau2 = t2_amps;
einsum(0.25, index::Indices{index::i, index::j, index::a, index::b}, &tau2, 0.5, index::Indices{index::i, index::a},
       t1_amps, index::Indices{index::j, index::b}, t1_amps);

// Compute the antisymmetrized two-electron integrals.
Tensor TEI_antisym = TEI;
permute(1.0, index::Indices{index::p, index::q, index::r, index::s}, &TEI_antisym, -1.0, index::Indices{index::p, index::q, index::s, index::r} TEI);

// Computing each term.
TensorView Fia = F(Range{0, n_occ}, Range{n_occ, n_orbs});
einsum(1.0, index::Indices{}, &E_ccsd, 1.0, index::Indices{index::i, index::a}, Fia, index::Indices{index::i, index::a}, t1_amps);

TensorView TEI_ijab = TEI_antisym(Range{0, n_occ}, Range{0, n_occ}, Range{n_occ, n_orbs}, Range{n_occ, n_orbs});
einsum(1.0, index::Indices{}, &E_ccsd, 1.0, index::Indices{index::i, index::j, index::a, index::b}, TEI_ijab, index::Indices{index::i, index::j, index::a, index::b}, tau2);

Runtime Comparisons#

Einsums is an easy to use library that is also quite fast. To show this, we benchmarked the code for the following equation used in quantum chemistry against several different methods.

\[J_{\mu\nu} = D_{\lambda\sigma}\left(\mu\nu\middle|\lambda\sigma\right)\]

\[K_{\mu\nu} = D_{\lambda\sigma}\left(\mu\lambda\middle|\nu\sigma\right)\]

\[G_{\mu\nu} = 2J_{\mu\nu} - K_{\mu\nu}\]

The code for the benchmarks can be found in devtools/profiling along with a spreadsheet containing the raw timings to update these images as we improve our algorithms. The benchmark was performed on a system with the following specifications.

CPU	Model	Intel Core i7-13700 K
	Clock	3.4 GHz
	Cache	30 MB
	Cores/Threads	16/24
GPU	Model	AMD Radeon RX 7900 XTX
GPU	Memory	24 GB
System	Memory	32 GB + 62 GB swap
	Storage	2 TB NVME SSD storage
	Operating System	Debian Bookworm
	Einsums Version	1.0-pre
	C++ Compiler	Clang 19.7.1
	Fortran Compiler	GCC Fortran 12.2.0
	BLAS Vendor	Netlib 3.9.0

The tensor contraction was performed in several different ways: for loops in C; for loops in C with OpenMP SIMD vectorization and parallelization; CONCURRENT DO loops in FORTRAN; BLAS gemv call for the J matrix and an explicit loop in C++ for the K matrix; BLAS gemv call for the J matrix, then permuting the two-electron integrals to allow for a gemv call to be used for the K matrix; Einsums without permuting the two-electron integrals for the K matrix; and Einsums with permutation of the two-electron integrals for the K matrix. This first image shows the breakdown of the timing for building the individual matrices. The build time for the G matrix is not included as its contribution is too small to see.

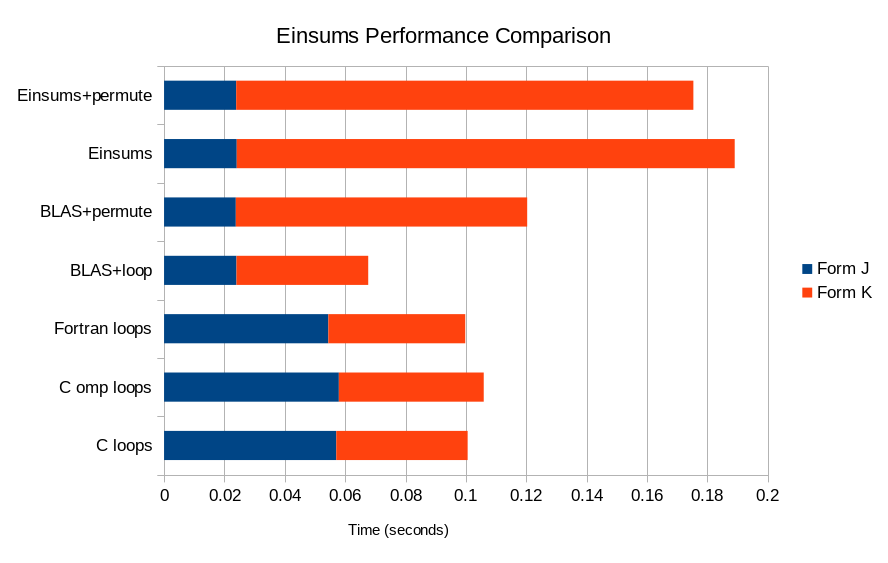
Breakdown of timings between various methods for contracting tensors.

As we can see, Einsums is a bit slower than raw BLAS, but still has comparable performance to a bare loop in C.

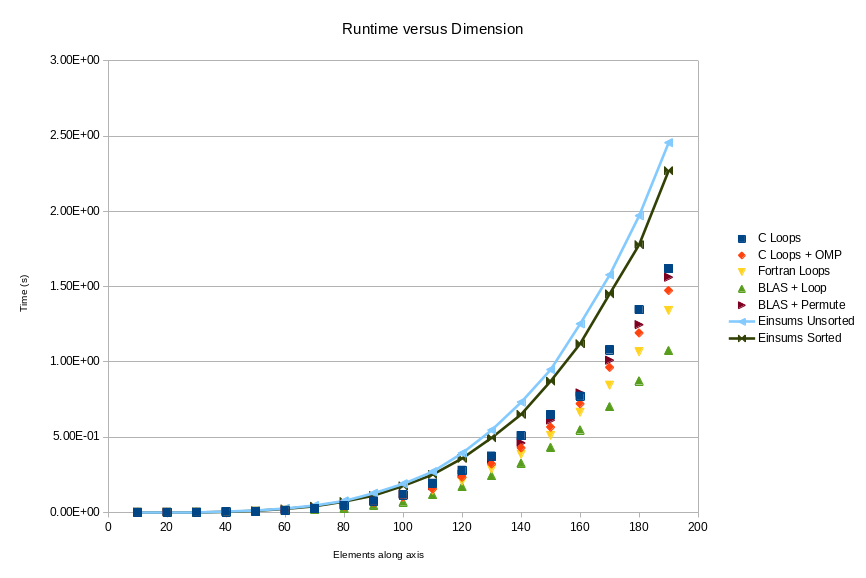
Comparison of timings based on tensor size.

In the above image, we can see how Einsums compares to the alternatives for various sizes of the input tensors. It seems to grow in a similar fashion to the alternatives.

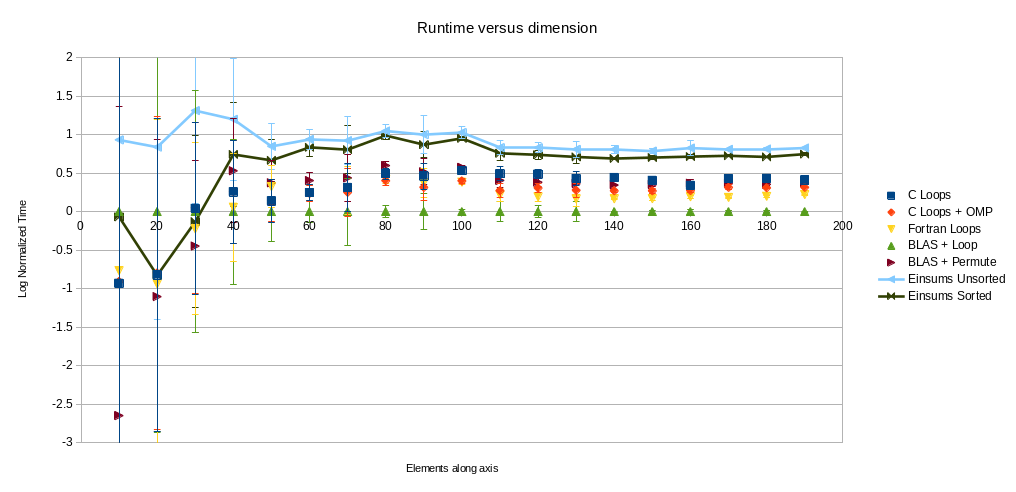
Rescaled comparisons of timings based on tensor size.

Since the previous graph is difficult to read for small sizes of the tensors, this provides a comparison that is normalized to the BLAS timings. Error bars are provided to show that the lower end is dominated by noise, and so the ordering might not be trustworthy.

Capabilities and Limitations#

As of right now, Einsums is capable of the following:

General contractions between two tensors of the form \(C_{ijk\cdots} = \alpha C_{ijk\cdots} + \beta A_{abc\cdots} B_{xyz\cdots}\).
Generalized transpositions of the form \(C_{ijk\cdots} = \alpha C_{ijk\cdots} + \beta A_{abc\cdots}\).
Linear algebra on tensors using BLAS and LAPACK as a backend.
Taking advantage of tensor layout. If the tensor is block diagonal or has blocks of zeros, the BlockTensor and TiledTensor classes can parallelize certain operations.
Mapping operations over all of a tensor’s indices.
Limited interaction with Python.
- A form of the einsum call works in Python. All Einsums functions exposed to Python can also consume NumPy arrays.
GPU acceleration for all of the above using HIP. Uses hipBLAS and hipSolver for the GPU linear algebra operations.
Simple arithmetic between tensors. The tensors all need to have the same dimensions, though, and this does not yet work on GPU.
Tensors representing functions of their indices.

The following is not supported, but may be supported in the future.

When calling einsum, there is no transposing of the indices. If a call can not be optimized without transpositions, it will use the generic algorithm rather than transpose indices until it can optimize the call.
Most simple arithmetic does not work on BlockTensor, TiledTensor, FunctionTensor, or any tensor for the GPU.
The Python module does not have any exposed linear algebra routines. This will be fixed in the future.
The Python module only supports contiguous tensors. It does not support block-sparse tensors, function tensors, or others.
The Python module interacts with Einsums in a completely different way than C++. Be careful of pitfalls when working with interoperable code.
Multi-node acceleration using MPI or similar.
Tensors stored on disk are not fully fleshed out yet, and the interface is not yet stable.